Trig (Trigonometry) Formulas and Notes
Special Angles
| Degrees | 0° | 30° | 45° | 60° | 90° |
| Radians | \displaystyle 0 | \displaystyle \frac{ \pi}{6} | \displaystyle \frac{ \pi}{4} | \displaystyle \frac{ \pi}{3} | \displaystyle \frac{ \pi}{2} |
| sin(x) | \displaystyle 0 | \displaystyle \frac{1}{2} | \displaystyle \frac{ \sqrt{2} }{2} | \displaystyle \frac{ \sqrt{3} }{2} | \displaystyle 1 |
| cos(x) | \displaystyle 1 | \displaystyle \frac{ \sqrt{3} }{2} | \displaystyle \frac{ \sqrt{2} }{2} | \displaystyle \frac{ \sqrt{1} }{2} | \displaystyle 0 |
| tan(x) | \displaystyle 0 | \displaystyle \frac{ \sqrt{3} }{3} | \displaystyle 1 | \displaystyle \sqrt{3} | - |
Law of Sines and Cosines
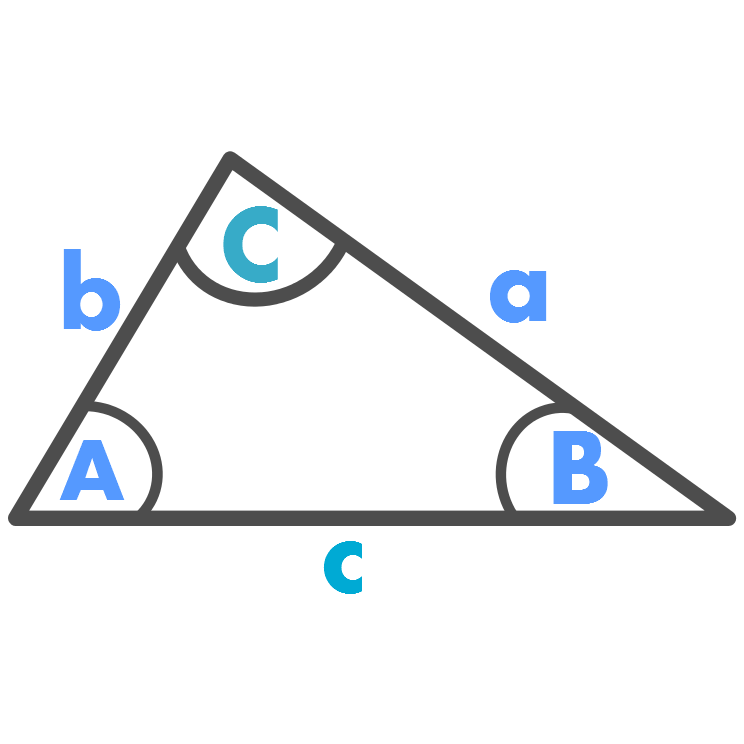
Law of Sines
\displaystyle \frac{\sin(A)}{a} = \frac{\sin(B)}{b} = \frac{\sin(C)}{c}
Law of Cosines
\displaystyle a^2 = b^2+c^2-bc{\cos(A)}
\displaystyle b^2 = a^2+c^2-ac{\cos(B)}
\displaystyle c^2 = a^2+b^2-ab{\cos(C)}
Identities
\displaystyle \sin^2(\theta)+\cos^2(\theta) = 1
\displaystyle \sec(\theta) = \frac{1}{\cos(\theta)}
\displaystyle \csc(\theta) = \frac{1}{\sin(\theta)}
\displaystyle \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}
\displaystyle \cot(\theta) = \frac{\cos(\theta)}{\sin(\theta)}
\displaystyle 1+\tan^2(\theta) = \sec^2(\theta)
\displaystyle 1+\cot^2(\theta) = \csc^2\theta
\displaystyle \sin(-\theta) = -\sin(\theta)
\displaystyle \cos(-\theta) = \cos(\theta)
\displaystyle \tan(-\theta) = -\tan(\theta)
\displaystyle \csc(-\theta) = -\csc(\theta)
\displaystyle \sec(-\theta) = \sec(\theta)
\displaystyle \cot(-\theta) = -\cot(\theta)
\displaystyle \sin(a \pm b) = \sin(a)\cos(b) \pm \sin(b)\cos(a)
\displaystyle \cos(a \pm b) = \cos(a)\cos(b) \pm \sin(a)\sin(b)
\displaystyle \tan(a \pm b) = \frac{\tan(a) \pm \tan(b)}{1 \pm \tan(a)\tan(b)}
\displaystyle \sin(2\theta) = 2\sin(\theta)\cos(\theta)
\displaystyle \cos(2\theta) = \cos^2\theta-\sin^2\theta
\displaystyle \cos(2\theta) = 1-2\sin^2(\theta)
\displaystyle \cos(2\theta) = 2\cos^2(\theta)-1
\displaystyle \tan(2\theta) = \frac{2\tan(\theta)}{1-\tan^2(\theta)}
\displaystyle \sin^2(\theta) = \frac{1-\cos(2\theta)}{2}
\displaystyle \cos^2(\theta) = \frac{1+\cos(2\theta)}{2}
