Coordinate / Analytical Geometry Formulas and Notes

Equation of a Line

Example
Find the equation of the line that passes through (5, 12) with a gradient of 4.
\displaystyle y-y_{1}=m \left( x-x_{1} \right)
\displaystyle y-(12)=(4) \left( x-(5) \right)
\displaystyle y-(12)= 4x-20
\displaystyle y= 4x-8

Equation of a Circle

Example
Find the equation of a circle with a radius of 5 centered at (-3, 2).
\displaystyle (x-a)^{2}+(x-b)^{2}=r^{2}
\displaystyle (x-(-3))^{2}+(x-(2))^{2}=5^{2}
\displaystyle (x+3)^{2}+(x-2)^{2}=5^{2}
\displaystyle (x+3)(x+3) + (y-2)(y-2)=25
\displaystyle x^{2}+y^{2}+6x-4y+13=25
\displaystyle x^{2}+y^{2}+6x-4y-12=0

Distance Formula

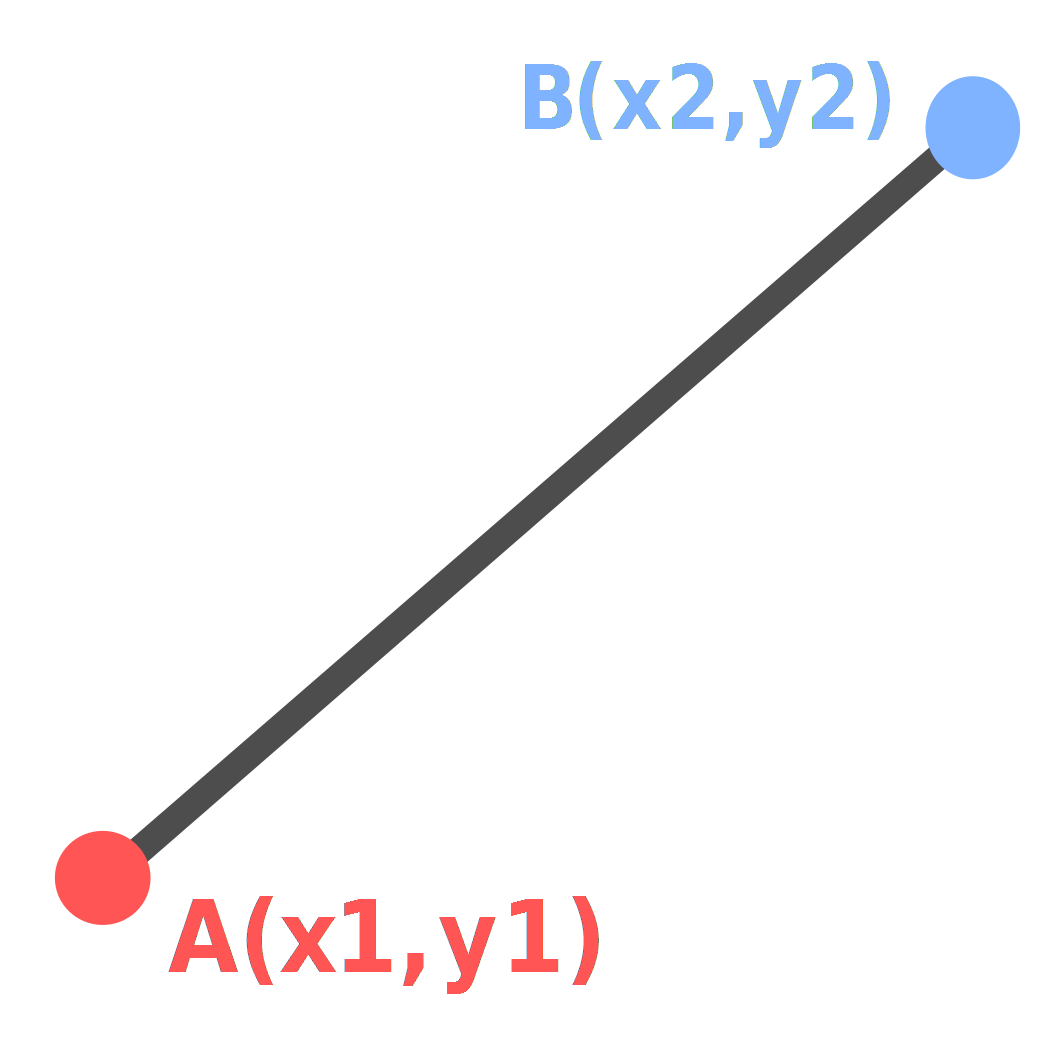
Example
Find the distance between (-3, 2) and (4, 8).
\displaystyle d = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}
\displaystyle d = \sqrt{(4--3)^2+(8-2)^2}
\displaystyle d = \sqrt{7^2+6^2}
\displaystyle d = \sqrt{49+36}
\displaystyle d = \sqrt{85}
\displaystyle d = 9.2195444573

Midpoint Formula

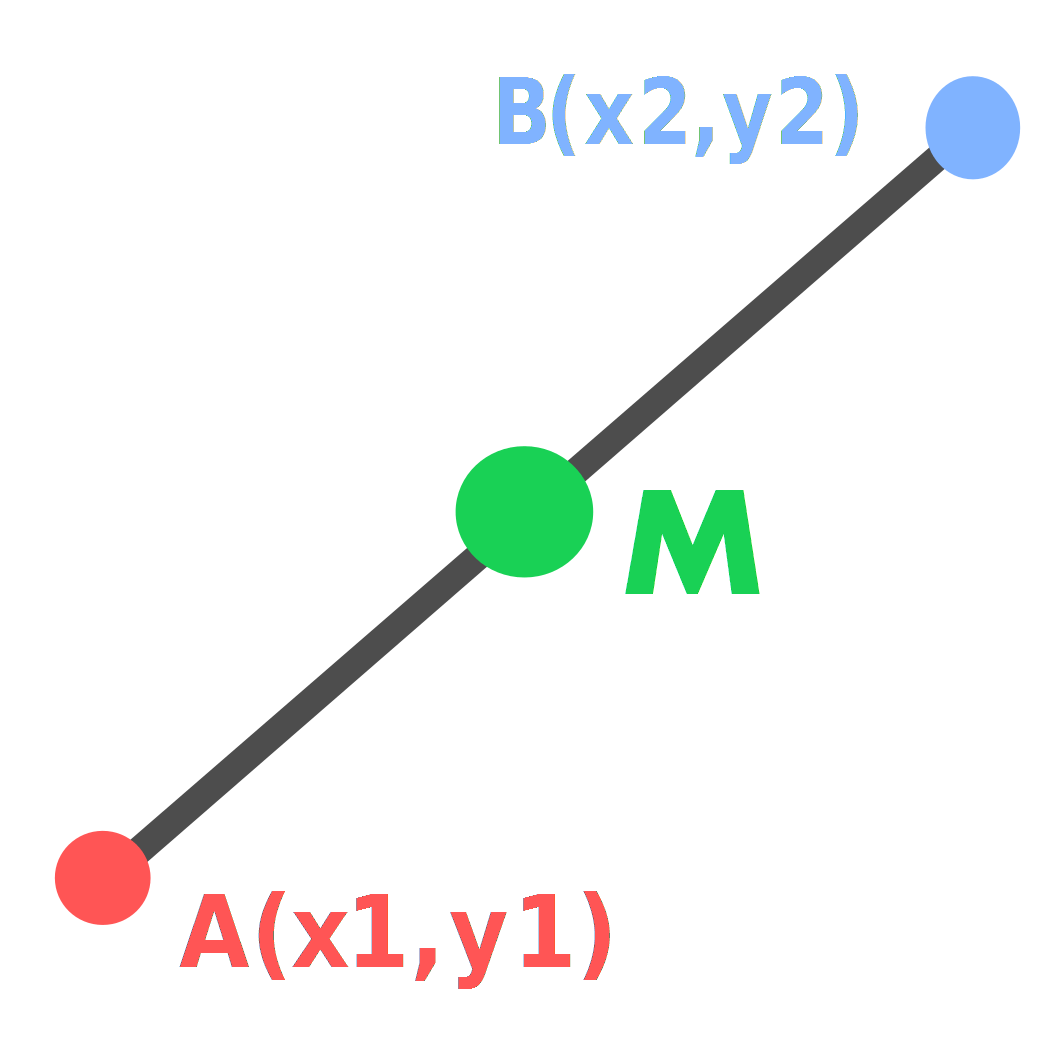
Example
Find the midpoint between (-3, 2) and (4, 8).
\displaystyle M \left( \frac{x_{1}+x_{2}}{2}; \frac{y_{1}+y_{2}}{2} \right)
\displaystyle M \left( \frac{-3+4}{2}; \frac{2+8}{2} \right)
\displaystyle M \left( \frac{1}{2}; \frac{10}{2} \right)
\displaystyle M \left( 0.5; 5 \right)

Gradient

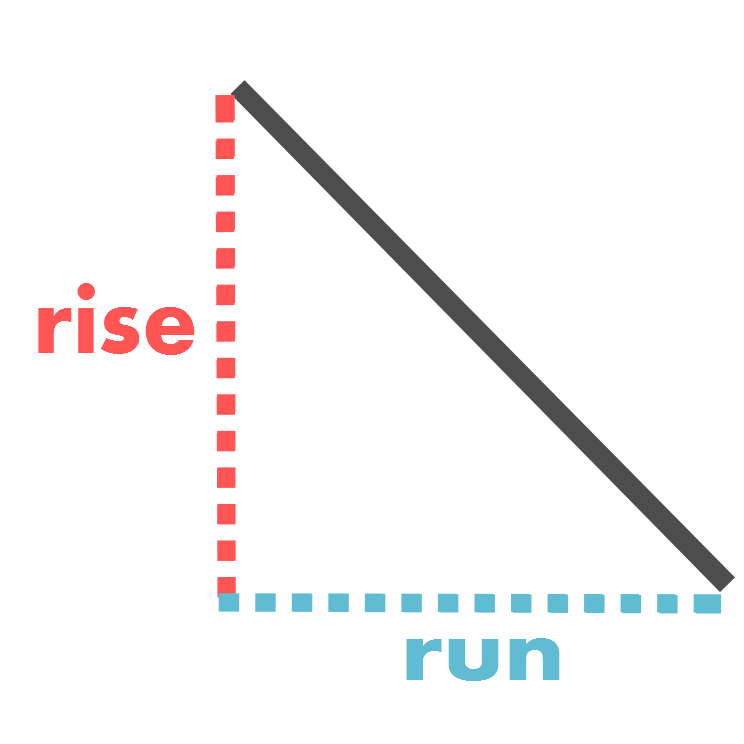
Example
Find the gradient between (-3, 2) and (4, 8).
\displaystyle m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}
\displaystyle m = \frac{8-2}{4--3}
\displaystyle m = \frac{6}{7}

Example
Find the gradient of a line with an inclination of 39°.
\displaystyle m = \tan( \theta )
\displaystyle m = \tan( 39 \degree )
\displaystyle m = 0.8099