Triangles Formulas and Notes

Contents

Types Triangles Properties of Triangles Right Angle Triangles Exterior Angles Similarity Congruence Median of a Triangle Altitude of a Triangle

Types of Triangles

Equilateral Triangle

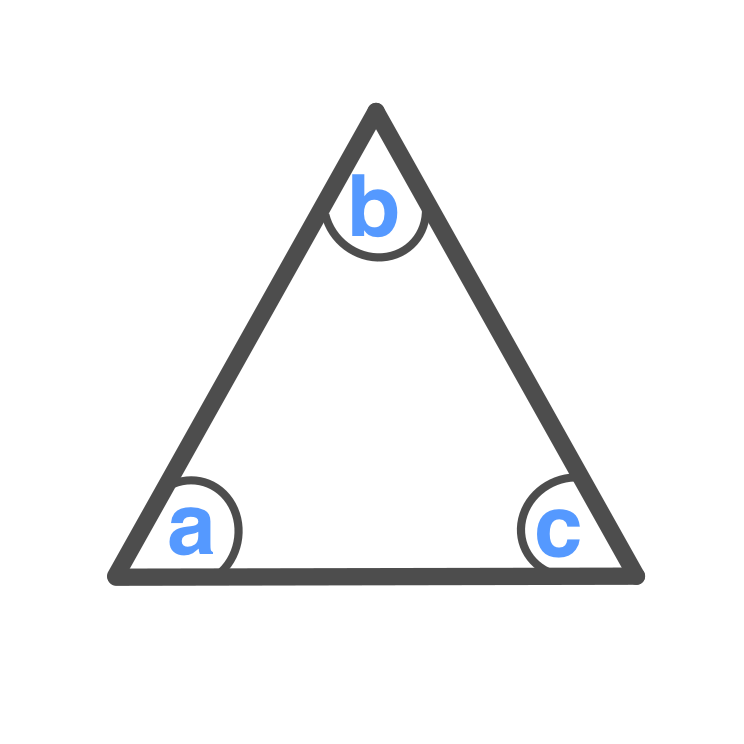
All sides are equal. All angles are equal to 60 °
\displaystyle a = b = c = 60 \degree

Scalene Triangle

Angles are not equal. Sides are not equal.

Isosceles Triangle

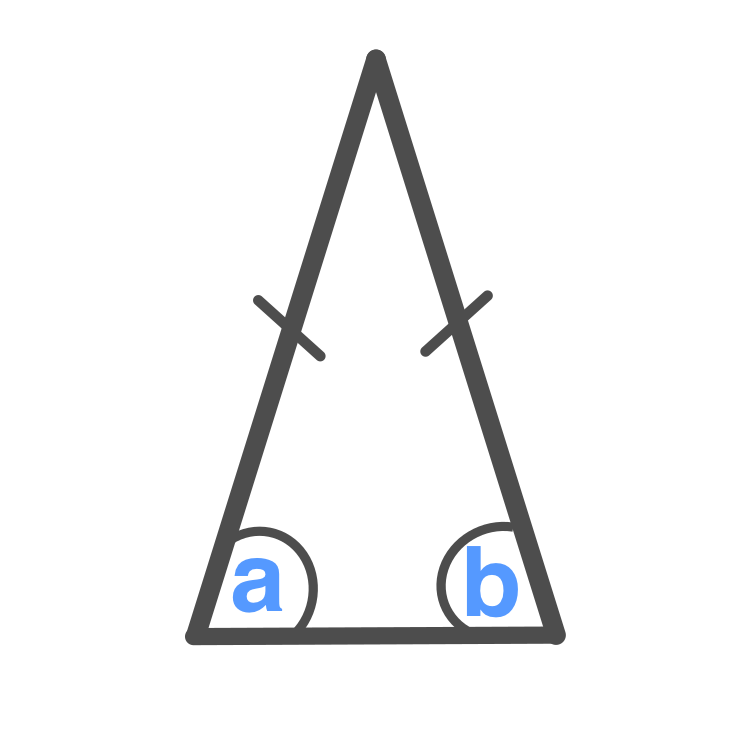
Two sides are equal. Two angles are equal.

a = b

Acute Triangle

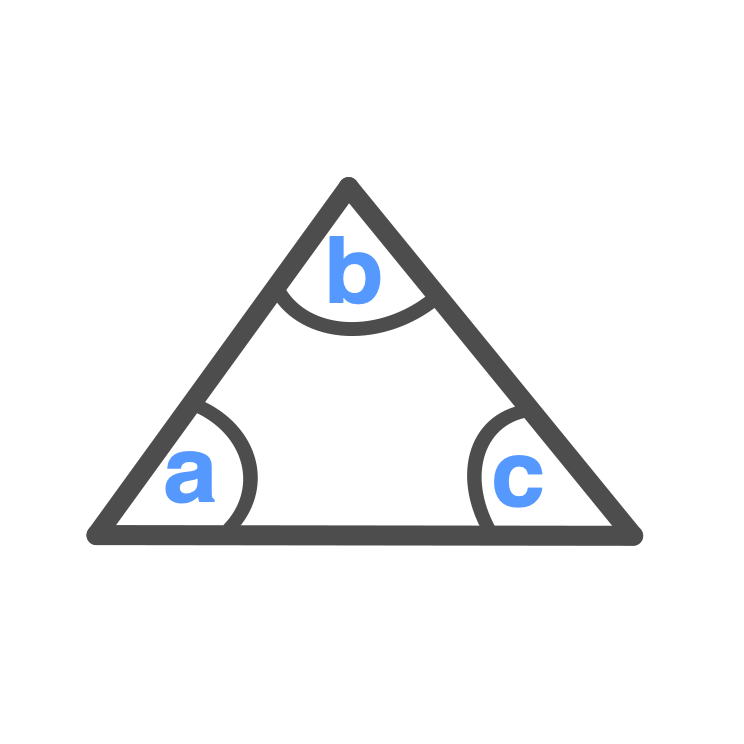
All angles are less than 90 °

\displaystyle a < 90 \degree ,b < 90 \degree ,c < 90 \degree

Obtuse Triangle

A triangle with an angle greater than 90°

\displaystyle x > 90 \degree

Right Angle Triangle

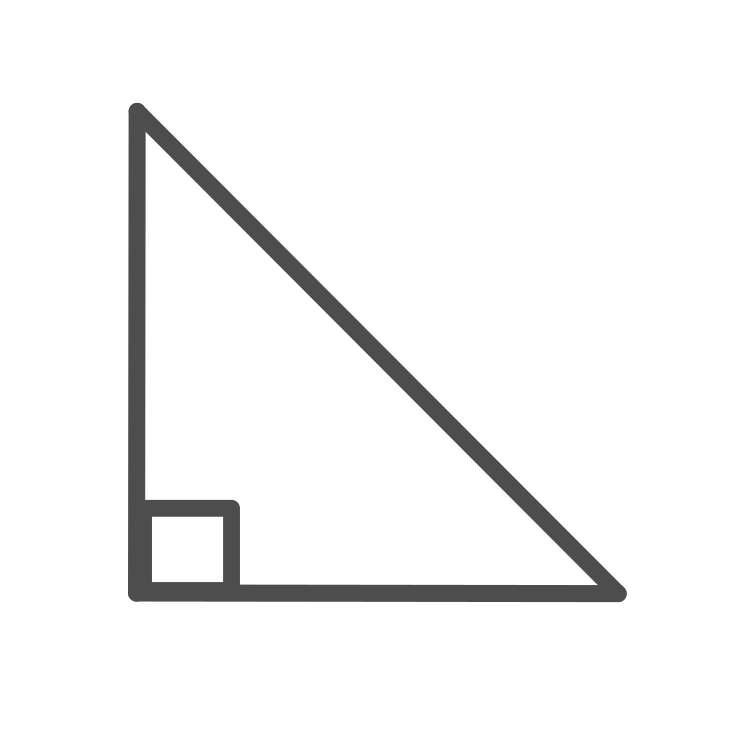
A triangle with an angle that is equal to 90°

Properties of Triangles

Sum of Angles

Angles in triangle have a sum of 180°

\displaystyle a + b + c = 180 \degree

Area

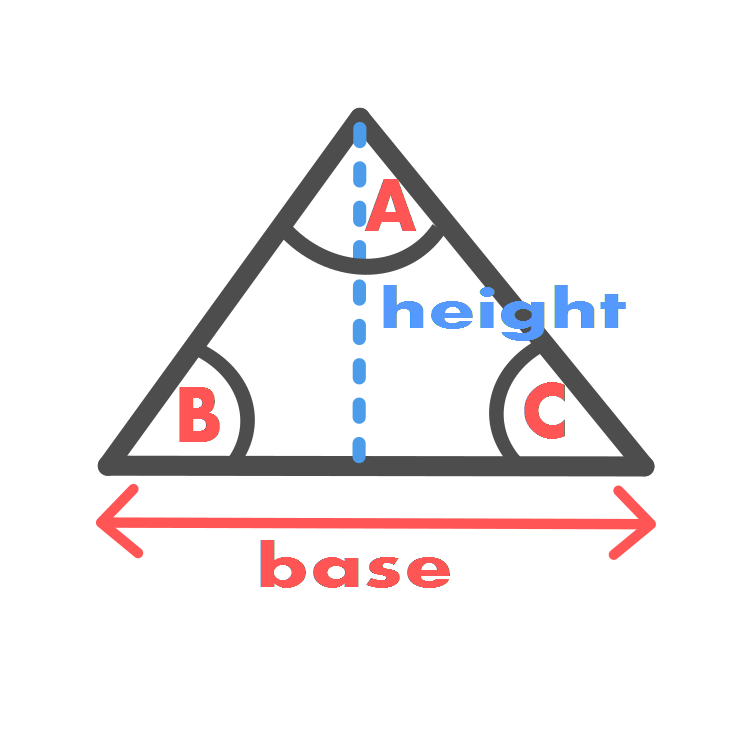
Area \displaystyle = \frac{1}{2} base × height

Area \displaystyle = \frac{1}{2} bc \sin(A)
\displaystyle = \frac{1}{2} ab \sin(C)
\displaystyle = \frac{1}{2} ac \sin(B)

Right Angle Triangles

Theorem of Pythagoras

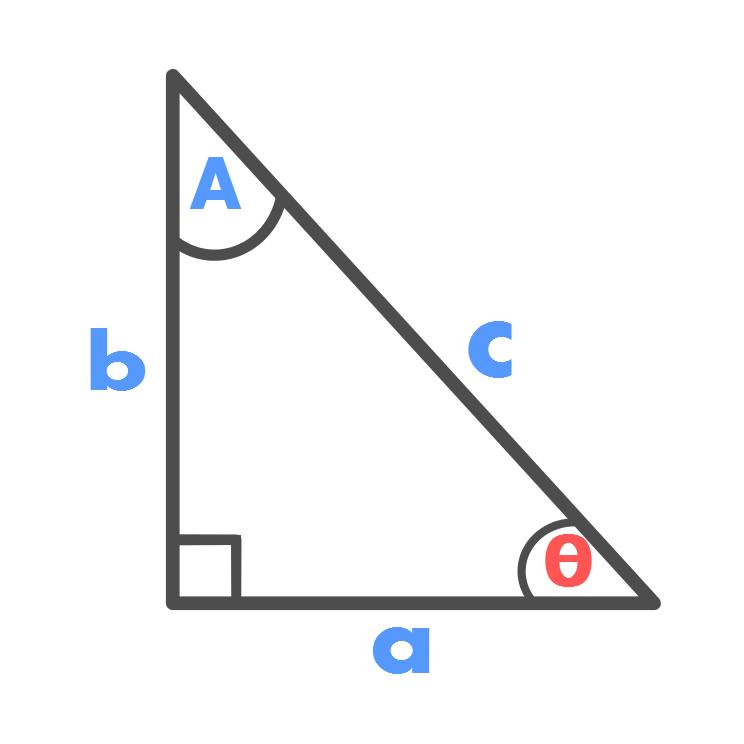
\displaystyle a^{2} + b^{2} = c^{2}

\displaystyle \rightarrow c = \sqrt{a^{2} + b^{2}}

\displaystyle \rightarrow a = \sqrt{c^{2} - b^{2}}

\displaystyle \rightarrow b = \sqrt{c^{2} - a^{2}}

Finding Missing Angles and Sides

using trig to solve Missing Angles and Sides of a triangle

\displaystyle \sin(\theta) = \frac{opp}{hyp}

\displaystyle \cos(\theta) = \frac{adj}{hyp}

\displaystyle \tan(\theta) = \frac{opp}{adj}

Exterior Angles

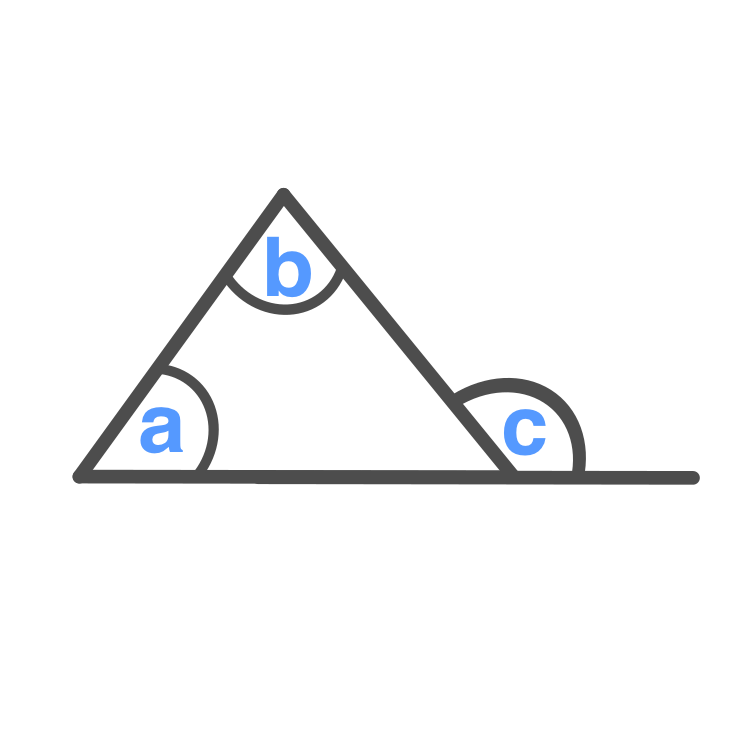
\displaystyle c = a + b

Similarity

Triangles are similar if they have the same exact shape but not necessarily the same size.

1.Corresponding angles have the same measure.

2.Corresponding sides are proportional to each other.

Angle-Angle-Angle

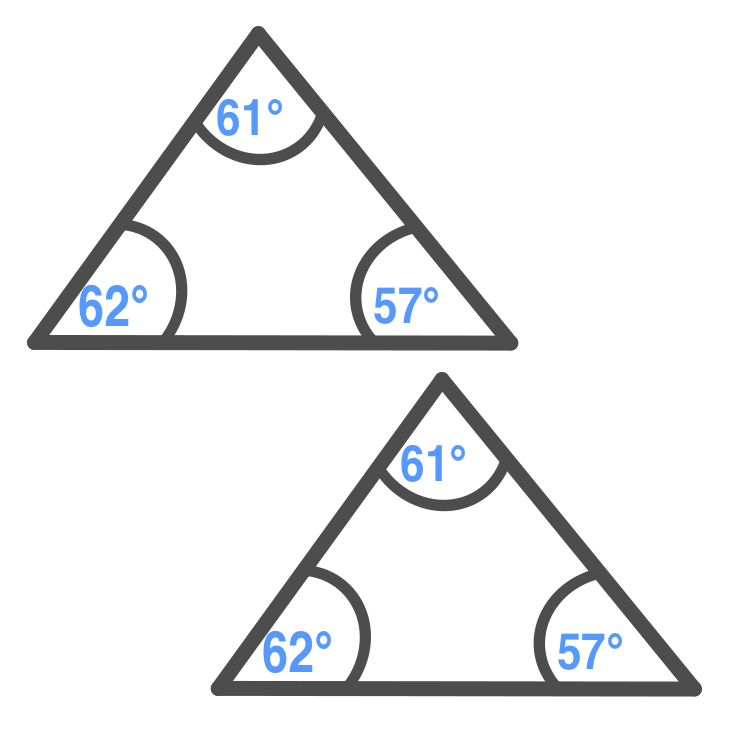
Triangles are similar if 3
pairs of triangles have
the same measure.

Side-Side-Side

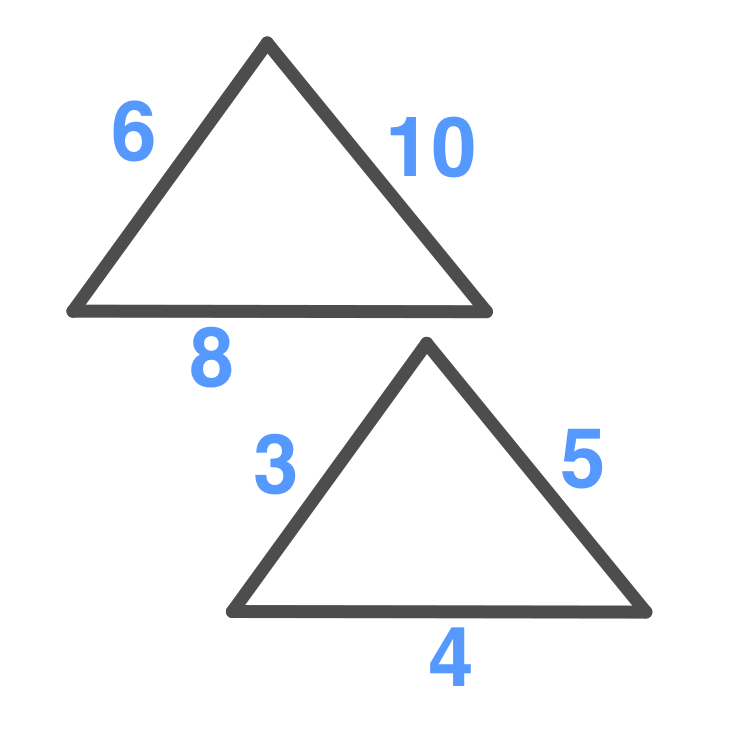
Triangles are similar if all
3 pairs of corresponding
sides are proportional.

Side-Angle-Side

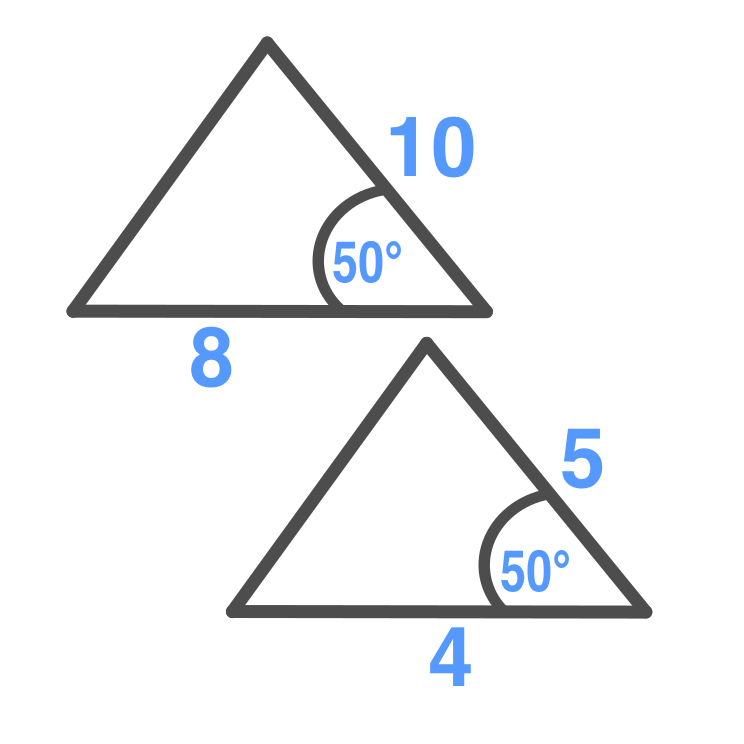
Triangles are similar if
two pairs of corresponding
sides are proportional and the
included angles have the
same measure.

Congruence

Triangles are congruent if they have the same exact size and shape.

Side-Side-Side

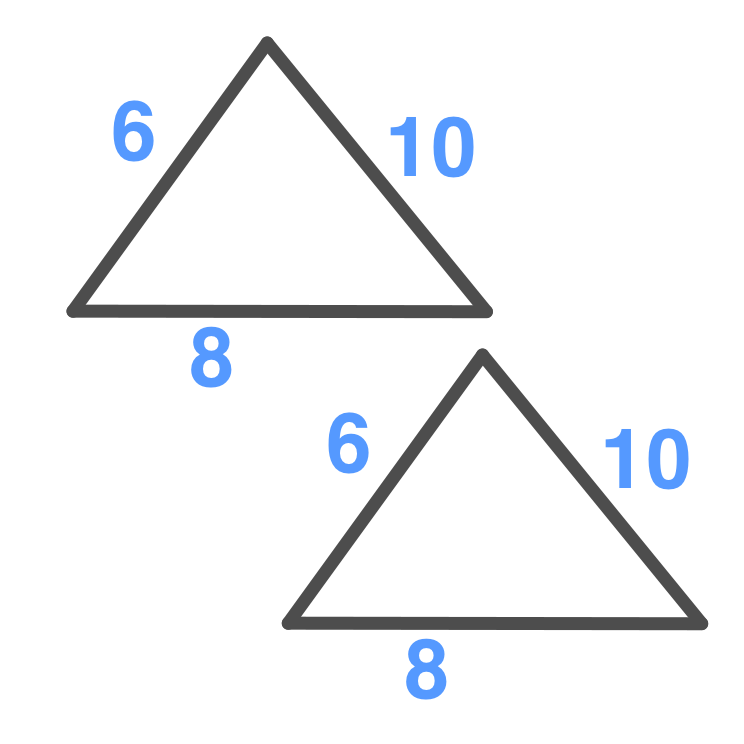
Triangles are congruent if all
3 pairs of corresponding
sides have the same measure.

Side-Angle-Side

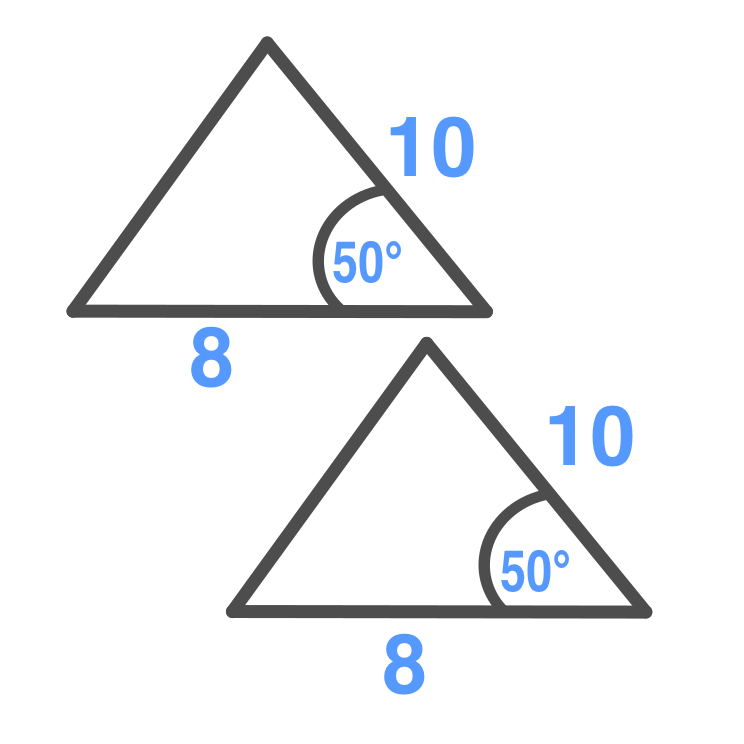
Triangles are congruent if
two pairs of corresponding
sides have the same measure and the
included angles have the
same measure.

Angle-Side-Angle

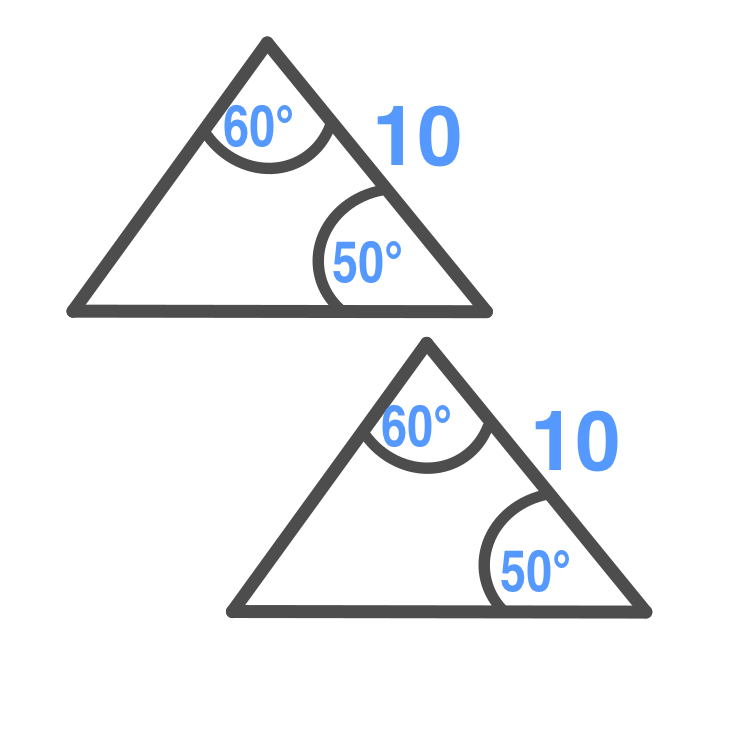
Triangles are congruent if
two pairs of corresponding
angles have the same measure and the
included sides have the
same measure.

Right Angle Hypotenuse

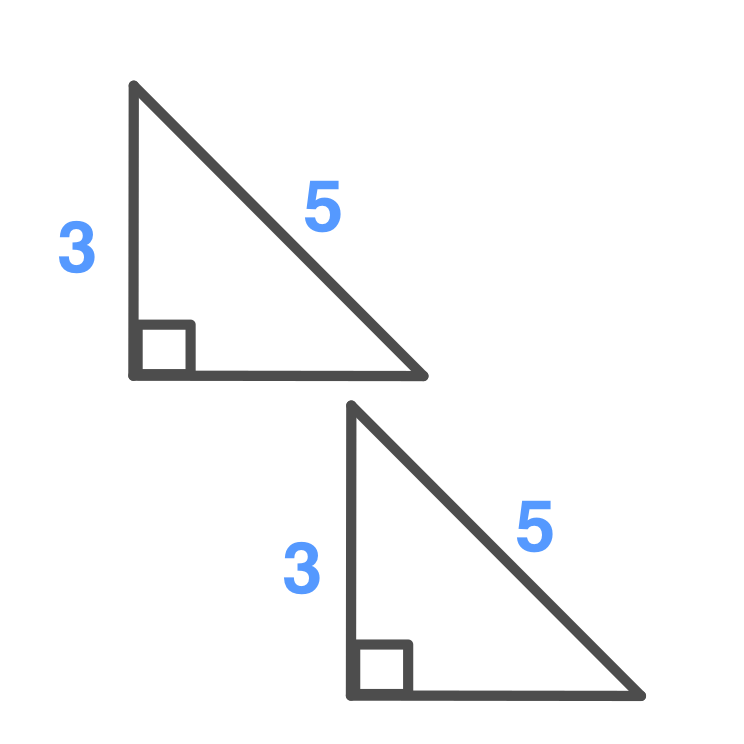
Triangles are congruent if
the corresponding hypotenuses
have the same measure and a
pair of other sides have the
same measure.

Median of a Triangle

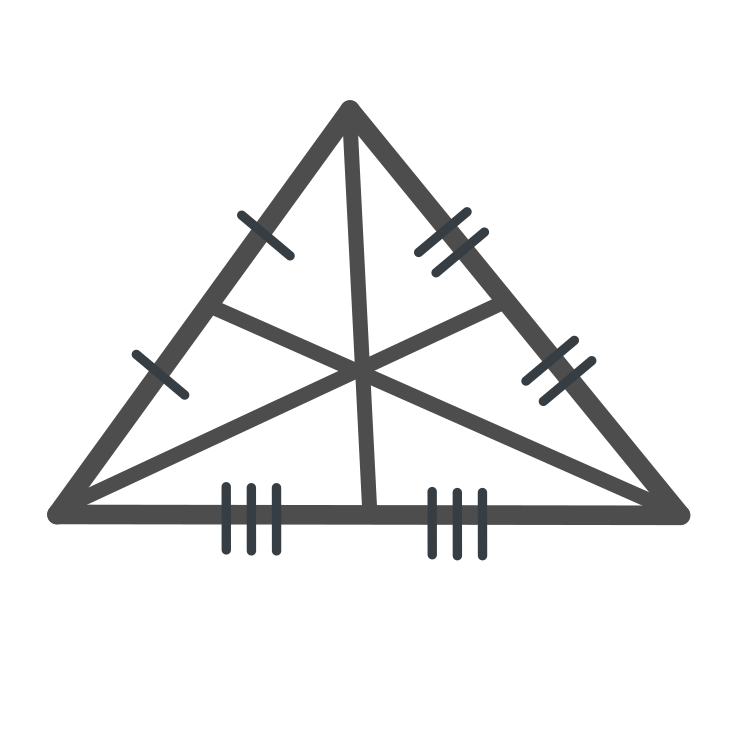
A median of a triangle is a line segment joining a vertex to the opposite side, bisecting it.

Altitude of a Triangle

A median of a triangle is a line segment through a vertex and perpendicular to a line containing the opposite side.